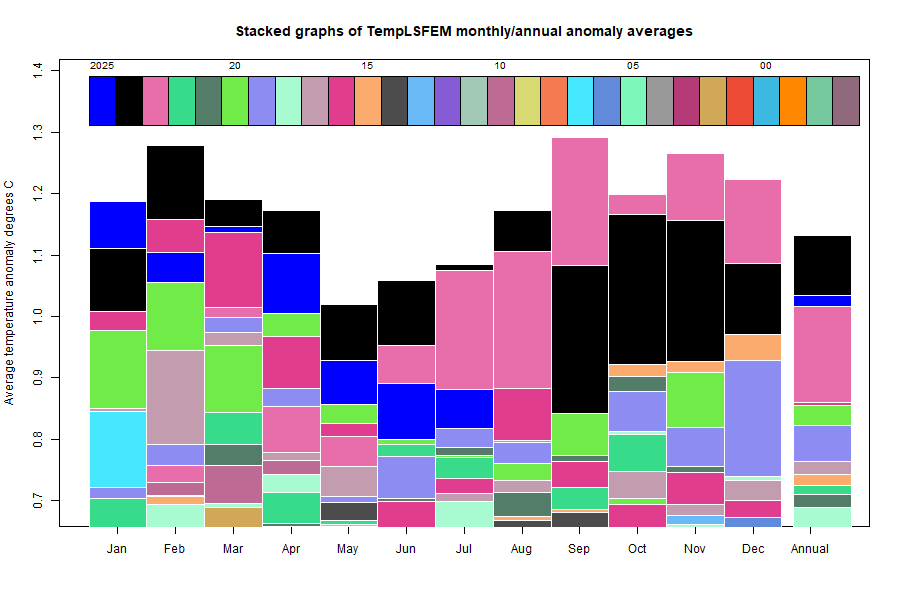
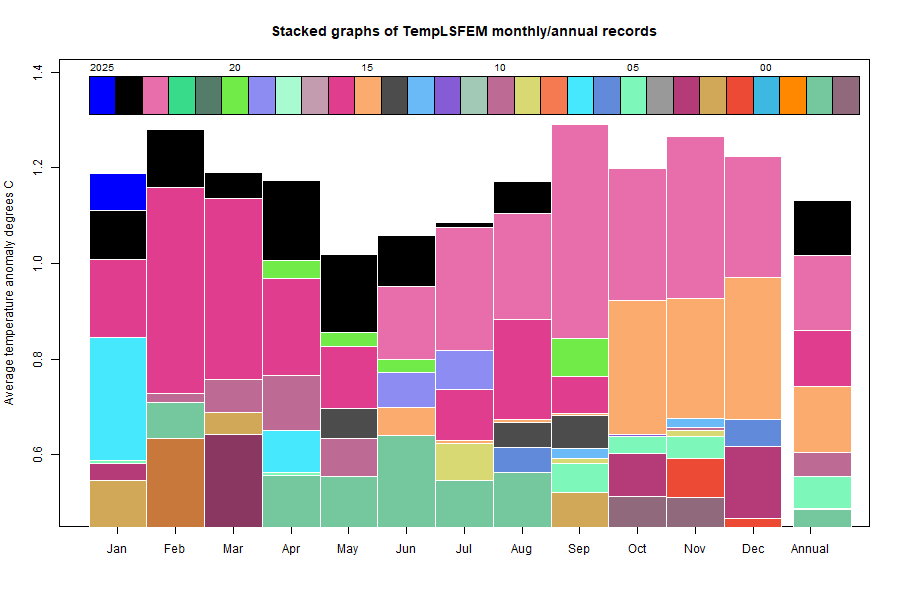
The GISS V4 land/ocean temperature anomaly was 1.39°C in March, down from 1.44°C in February. This fall is smaller than the 0.11°C fall reported for TempLS.
As with TempLS, March was the warmest March in the record - next was 1.35°C in 2016. It was the fourth warmest month of all kinds.
As usual here, I will compare the GISS and earlier TempLS plots below the jump.
The Green Agenda Will Lead to Civil War
1 hour ago