That is a point I was emphasising in this post on homogenisation. The average is little affected by unbiased noise (cancellation), but sensitive to bias. So it makes sense to identify and eliminate bias, even if it increases noise. Homogenise.
There is another common naysayer claim, that averages are not more accurate than the original readings, as in this WUWT thread. I don't know what they think drug companies etc go to great expense to get a large set of responses to average.
Anyway, in this post I'll give a dramatic demonstration of the noise suppression of averaging. I'll take the usual post-1900 monthly GHCN and ERSST data and let TempLS calculate an annual average. Then I'll add Gaussian noise to every single monthly average. Big noise - amplitude (sd) 1 °C. That's a world in which thermometers can barely be read to the nearest degree. In fact much worse, since monthly averaging already reduces noise. Then I'll recompute and show the differences in various ways. I'll do 10 instances.
As you'll guess, the difference is small. The standard deviation of fluctuations about the unperturbed is about 0.006 °C. The effect on trend is even smaller. The unperturbed trend 1900-2014 is 0.7073 °C/Century and the range is about 0.705 to 0.710.
I should emphasise that this perturbation operates on what might be taken to be measurement error, and does not emulate that quoted by NASA, NOAA etc, which is dominated by spatial sampling error. It also assumes white (ie independent) noise; dependence will increase the effect. But from a very low base.
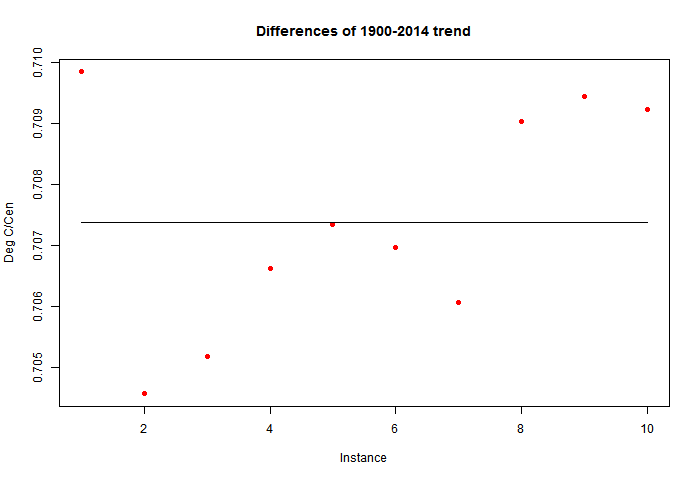
So here is the plot of time series of a single perturbation (red) against unperturbed. The change is barely visible. 1°C unbiased noise added to the individual monthly averages makes scarcely any difference.
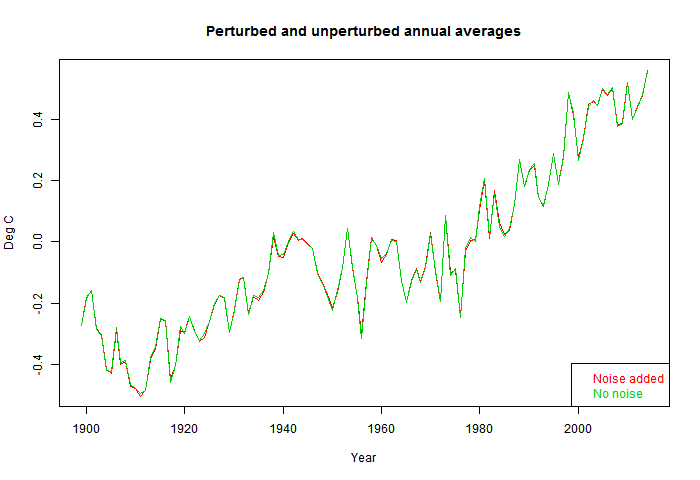
So I'll plot the differences over time. This time I'll show the 10 instances - the signal is effectively random. The horizontal lines show the mean and 1 sd range. Note the y-axis scale.
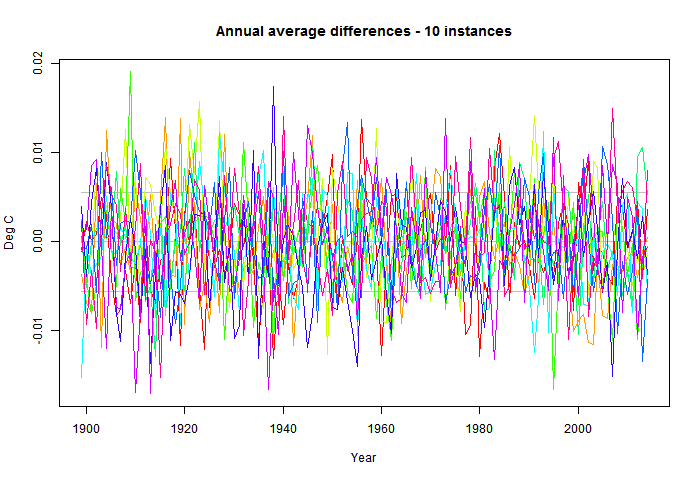
Finally I'll show a plot of 1900-2014 trends. As mentioned, the unperturbed is 0.7073 and the range about +-0.0025; about 0.4%.













And a 1 degree error in the monthly means would correspond to an about 5 degree error in the daily values. The error of the monthly values is 5.5 times (square root of 30 = 5.5 ) smaller than the error in the daily values.
ReplyDeleteLike you say, what matters is bias.
Nick a related issue is when you apply a homogenization correction to what amounts to noise, but is not resolvable in the global average, what you'd effectively done is trade spatial resolution for an unresolvable change in the global average.
ReplyDeleteI think this is the chief problem with BESTs empirical homogenization algorithm by the say, and why they end up getting South America to warm and cool as a single body. (Even we have the Andes mountains undergoing deglaciation and Amazon rainforest being systematically harvested by humans over the last century, which should lead to observable variability in the rate of warming of that continent.)
Nick, your "empirical" demonstration is much appreciated. My occasional attempts to persuade contrarians using the theory of combination of errors in quadature that the error of the sample mean will vary as 1/square root(N) for N the sample have got me nowhere. The rebuttal is either that I'm "just playing with algebra" rather than using "real data" or something on the lines that the 1/root(N) rule only applies to repeat measurements on the same object, so the rule doesn't apply to averaging measurements from different places. Your simulation appears to be more difficult to dismiss, though I'm sure people will do their utmost to find a refutation.
ReplyDeleteBe sure that nature knows how to make quick adjustments in the global temperatures to maintain a proper equilibrium.
ReplyDeleteANyway, if we force the environment too much, nature has also the tools to cool us down very quick.
"I don't know what they think drug companies etc go to great expense to get a large set of responses to average."
ReplyDeleteWould you mind amplifying that remark, and explaining why you think it's a good analogy? Thanks.
It refers to the fact that when you are seeking to measure a response subject to a great deal of natural variation, you get a better estimate from averaging a large sample, even though, in the case of drug trials, that is expensive.
DeleteFixed typos:
DeleteThank you. That's what I figured you must mean. But why is that a good analogy?
By "response" in the case of drug trials, I suppose you mean a range of results from "no effect" or "successful treatment" through to "unintended death" and all the many possibilities in between. One would indeed get a better idea of the range of the drug's results (whether intended or unintended; whether good, bad, or indifferent) by conducting trials on a larger number of patients.
I don't see why that's a good analogy to averaging temperature readings.
Unless I am misunderstanding what goes on in such experiments, I don't see that any averaging is done in the case of drug trials: they are finding out what the possible results are, and how they are distributed among the test subjects. To simplify, say 10,000 subjects: 2,000 no effect, 3,000 simple success, 3,000 success with minor side effects, 2,000 success with serious side effects.
From that, they would extrapolate to the general population, or at least to the larger population for whom the drug is intended. Right?
Where's the averaging?
"they are finding out what the possible results are, and how they are distributed among the test subjects. "
DeleteEstimating a distribution, as you are doing, involves binning. You are estimating the numbers in those classes; effectively, the mean of a Poisson distribution. So the accuracy of those depends on sample sizes. The results you cite would be more convincing than if you had 10 subjects, with 3 simple success etc. That's what they pay for.
But trials can be more quantitative. Of two drugs, which gives the greater lowering of blood pressure? Which gives a greater lowering of stomach acidity? Which gives longer survival times? All use averaging to improve the accuracy of the estimate.
Thank you.,
Delete